Multi-Source SATEM 1D Inversion and Its Application to the 3D Model Data
-
摘要:
为了避免长导线源地空瞬变电磁装置的体积效应影响,并发挥装置探测深度大工作效率高的优势,分别设计了单个激发场源和多个激发场源的地空瞬变电磁数值模拟,对比分析场源分布对瞬变场的影响以及对地下模型的分辨特征。将一维反演应用于三维地电模型数据的解释之中,讨论复杂的激发源、简单的解释技术实现三维复杂目标反演的可行性。首先,采用三维数值模拟实现复杂激励源地空瞬变电磁三维正演模拟,分析多激励源瞬变场特征,证明可以通过改变源的布设方式减少电性源体积效应影响。然后,利用常规一维反演方法对数据进行解释,从而证明多源发射简单的解释方法也可以提高解释的分辨率。最后,对甘肃省某煤田采空区的野外数据进行一维反演解释,结果表明相较于单辐射源瞬变电磁的反演结果,使用多辐射源瞬变电磁探测方法可以得到更为精准的采空区分布信息。数值模型与实测数据解释结果充分说明复杂激发源即使采用简单的反演方法也能够有效提高解释结果的分辨率,这为提高瞬变电磁解释精度提供了新的思路。
Abstract:In order to avoid the volume effect of long-wire sources in semi-airborne transient electromagnetic device and leverage the advantages of high detection depth and working efficiency, numerical simulations were conducted using single and multiple field sources. The effect of source distribution on the transient fields and resolution characteristics of underground models was analyzed. The feasibility of achieving 3D complex target inversion using simple explanation techniques was discussed by applying the 1D inversion to interpret 3D geoelectric model data. First, the 3D FEM is used to realize the 3D forward modeling of multi-source semi-airborne TEM, analyze the characteristics of the multi-sources transient field, and prove that the volume effect of electrical sources can be reduced by changing the source layout. Then, the 1D inversion method is used to interpret the 3D model data to prove that the simple interpretation method of multi-source device can also improve the resolution of the result. Finally, 1D inversion interpretation of survey data from a coal mine goaf in Gansu Province is carried out. The results show that compared with the results of single-radiation source survey data, the multi-source survey data can be more accurate on the distribution of water zone. The interpretation of the synthetic model and the survey data demonstrate that the resolution of the results can be effectively improved even if simple inversion methods are used for complex excitation sources, which provides new ideas and useful explorations for improving the accuracy of TEM interpretation.
-
电性源地空瞬变电磁由Nabighian在水平电偶源的工作方式上发展而来,是瞬变电磁法的一种装置形式。由于利用接地长导线源在地表进行激发、在空中采用无人机平台携带接收装置进行数据采集,这种工作方式相较于航空瞬变电磁系统,不受飞行平台载重以及发射功率等限制,可以实现较大的探测深度;无人机飞行平台可实现快速三维数据采集,与地面瞬变电磁法相比,可大大提高测点密度及工作效率。因此地空瞬变电磁法可以兼顾地面装置探测深度大和航空装置工作效率高两大优点,是一种具有较大发展潜力的瞬变电磁方法。
由于地空瞬变电磁装置的诸多优点,近些年该方法得到了快速的发展,Fugro公司研制了TerraAir半航空时间域电磁系统,对比分析了航空系统、半航空系统以及地面装置接收信号的信噪比(Smith, 2001)。为了实现对深部矿产与地热资源的探测,Mogi等(1998)研制了基于直升机平台的GREATEM系统,并在火山结构调查、地热资源探测与海侵调查等方面取得良好效果(Mogi et al., 1998,2009;Allah et al., 2011, 2013; Ito et al., 2011, 2014)。林君等研制了一套地空瞬变电磁系统,它采用接地长导线作为发射源,无人飞艇或旋翼无人机作为载体搭载电磁接收系统(嵇艳鞠, 2013),该装置在地下水盐渍化及巷道采空区探测等方面取得了良好的应用效果,将该方法进行了进一步推广(李肃义 2013)。
目前,地空瞬变电磁解释方法主要基于单源瞬变电磁给出正反演算法以及近似解释方法(张莹莹, 2016)。多数学者通过改进优化算法或者采用成像方法提高解释精度(李貅,2015),也有学者分析了场源形式对瞬变电磁场的影响。Wright(2002)提出了MTEM方法,讨论不同的激发波对瞬变电磁场的影响,分析了电偶源瞬变电磁场的特征,提出轴向采集方式能够提供更多的信息。在探地雷达以及直流电阻率电法勘探(Bryan, 2015)等领域多源激发取得了较好的效果;李貅(2021)指出通过合理布置发射源可以提高探测深度,提高异常体分辨能力。鉴于此,文中利用有限元法进行多激励源三维模型瞬变电磁模拟,讨论多源激发场特征,采用传统的一维瞬变电磁反演方法对比分析单源数据与多源数据的反演结果。
总之,笔者通过开展多辐射源地空瞬变电磁方法的研究,利用组合多发源的工作方式,减小了体积效应的影响,提高对目标体的分辨能力,并通过传统的一维反演对多发射源组合效果进行了说明。
1. 多源地空瞬变电磁响应特征分析
多源响应特征可以直接从均匀半空间模型出发进行讨论,基于半空间模型响应特征指出源的不同组合形式可加强或者抵消某个场的分量,也可以利用三维正演基于复杂模型分析多源响应特征(张莹莹等,2016)。为了验证一维反演解释技术对复杂模型解释的适用性,文中从复杂模型出发利用三维数值模拟分析典型组合源的响应特征。
1.1 有限元三维正演原理
已知地空瞬变电磁满足的有限元变分方程,如式(1)所示:
$$ \int_V {\left[ {(\nabla \times f) \cdot (\nabla \times {\mathbf{E}}) + \sigma {\mu _0}f \cdot \frac{{\partial {\mathbf{E}}}}{{\partial t}} + {\mu _0}f \cdot \frac{{\partial {{\mathbf{J}}_{\rm{s}}}}}{{\partial t}}} \right]} dV = 0 $$ (1) 其中,f为矢量基函数;E为电场矢量;$ \sigma $为电导率;$ {\mu _0} $为真空磁导率;Js为源电流密度。
电场的时间离散如式(2)所示:
$$ \frac{{\partial {{\mathbf{E}}_{\mathbf{n}}}}}{{\partial {t_n}}} = \frac{{{{\mathbf{E}}_{\mathbf{n}}} - {{\mathbf{E}}_{{\mathbf{n - 1}}}}}}{{{t_n} - {t_{n - 1}}}} $$ (2) 将式(2)带到式(1)中,通过单元分析可将式(1)写成矩阵形式,如式(3)所示:
$$ {{\mathbf{A}}_{\mathbf{e}}}{\mathbf{E}}_{\mathbf{e}}^{\mathbf{n}} = {{\mathbf{b}}_{\mathbf{e}}} $$ (3) 其中,
$$ {{\bf{A}}_{\bf{e}}} = \int_V {\left[ {\left( {\nabla \times {N_i}} \right) \cdot \left( {\nabla \times {N_j}} \right) + \frac{{\sigma {\mu _0}}}{{{t_n} - {t_{n - 1}}}}{N_i} \cdot {N_j}} \right]} dV$$ $$ {{\bf{b}}_{\bf{e}}} = \frac{{\sigma {\mu _0}}}{{{t_n} - {t_{n - 1}}}}\int_V {{{\bf{E}}_{{\bf{n}} - {\bf{1}}}}} \cdot {N_i}dV - \frac{{{\mu _0}}}{{{t_n} - {t_{n - 1}}}}\int_V {\left( {{{\bf{J}}_{\bf{n}}} - {{\bf{J}}_{{\bf{n}} - {\bf{1}}}}} \right)} \cdot {N_i}dV$$ 式中:${\mathbf{E}}_{\mathbf{e}}^{\mathbf{n}}$为待求第n时刻的电场在单元的各棱边上投影值形成的列向量;$ {{\mathbf{J}}_{\mathbf{n}}} $为第n时刻源的电流密度。
求得电场后可利用电场计算磁场分量,文中仅讨论磁场垂直分量的感应电动势,其如式(4)所示:
$$ \frac{{\partial {{\mathbf{B}}_z}(t)}}{{\partial t}} = \frac{\partial }{{\partial y}}{{\mathbf{E}}_x} - \frac{\partial }{{\partial x}}{{\mathbf{E}}_y} $$ (4) 1.2 多源地空瞬变电磁响应特征分析
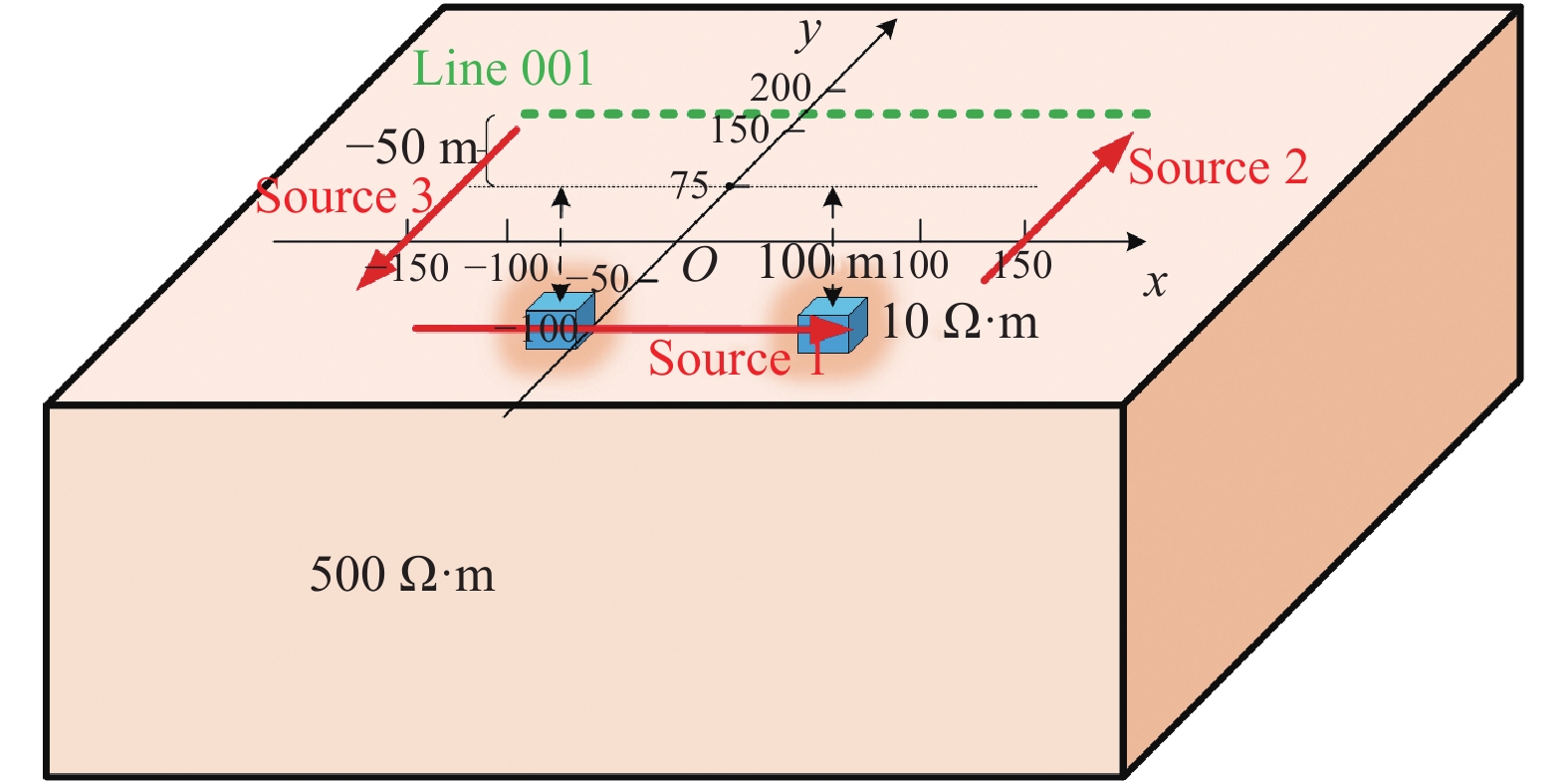
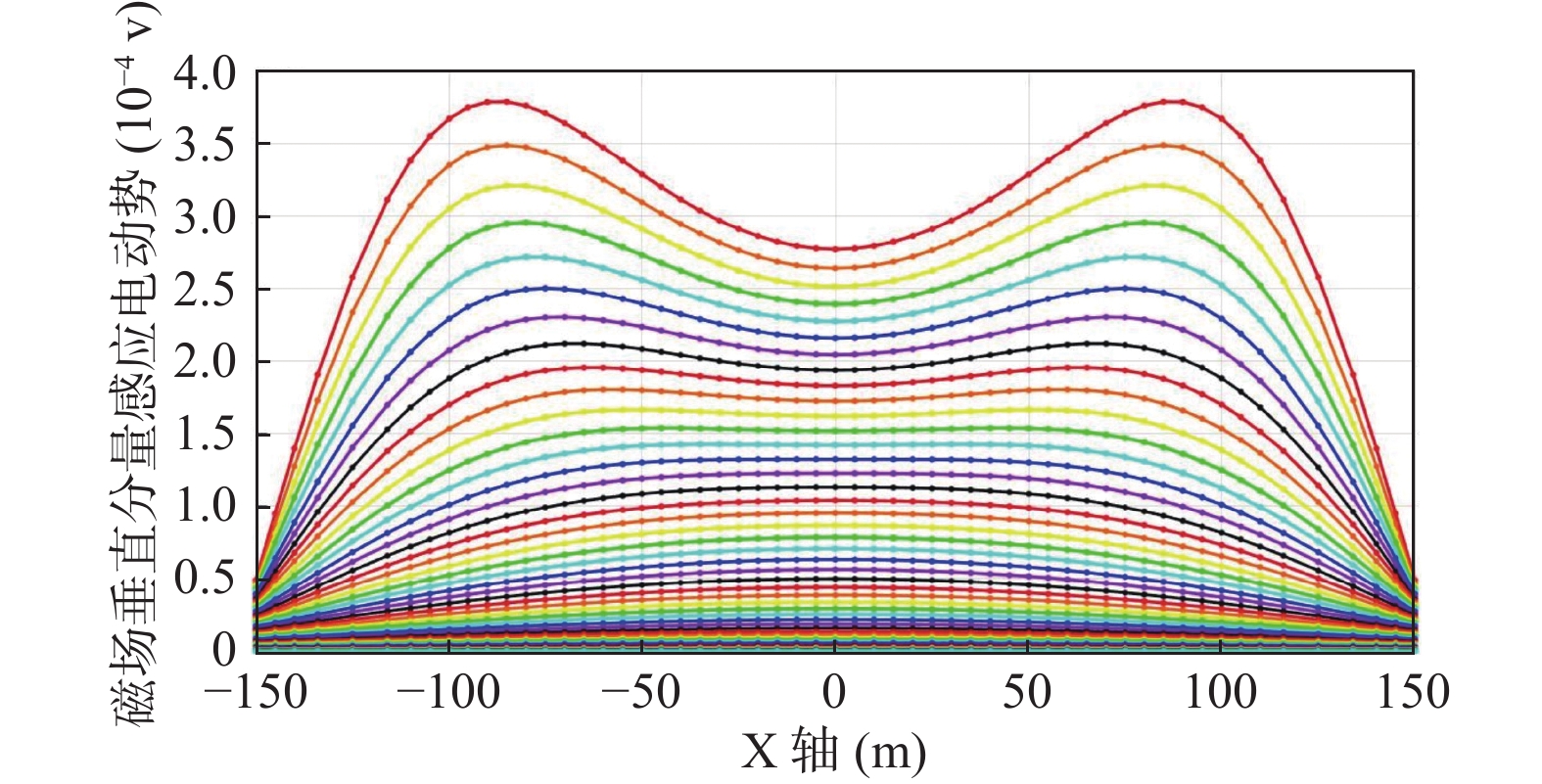
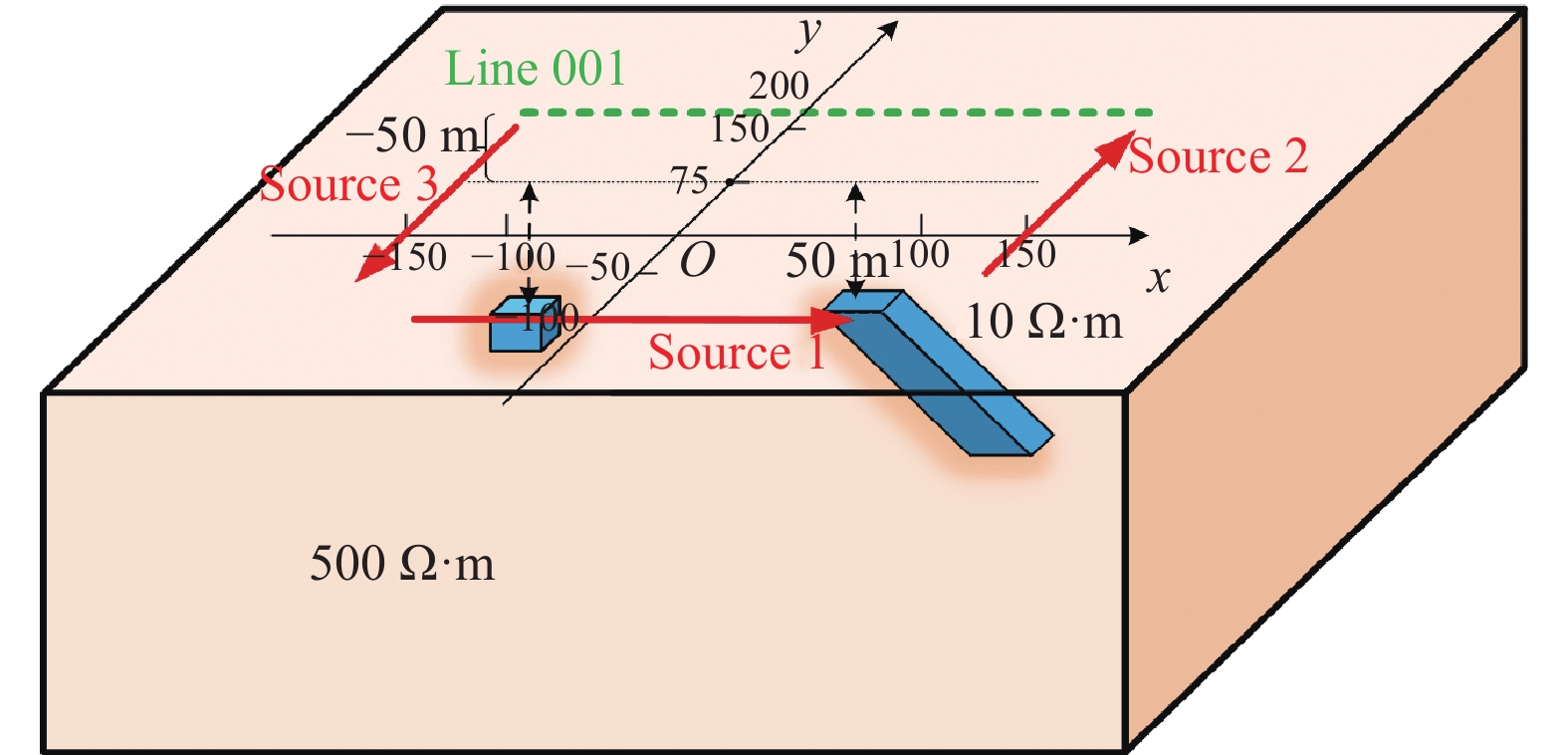
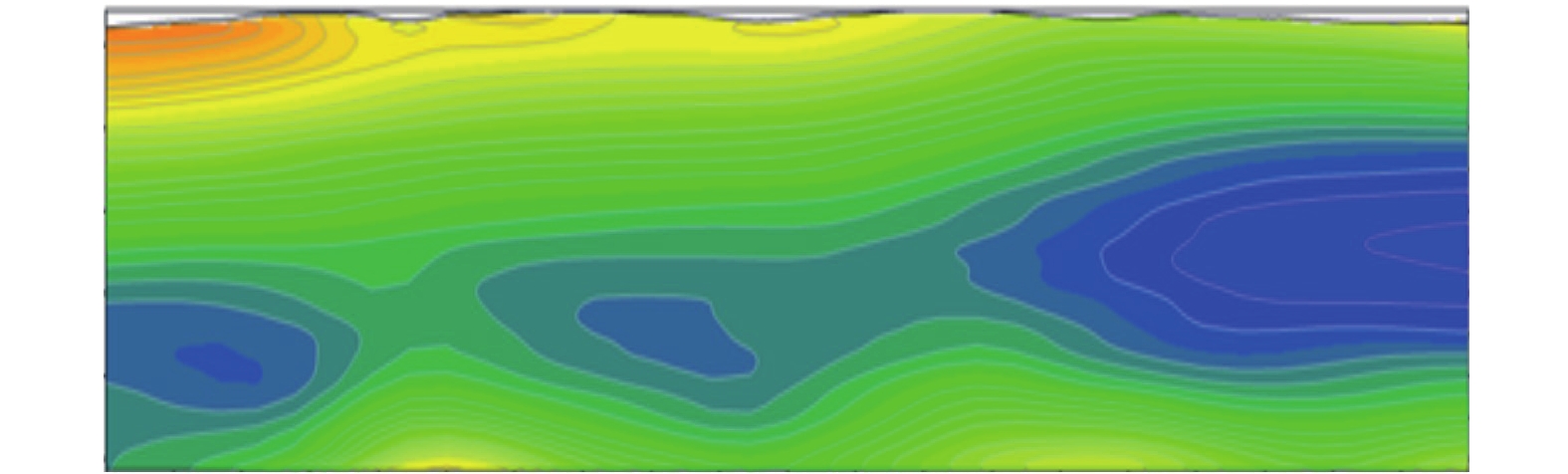
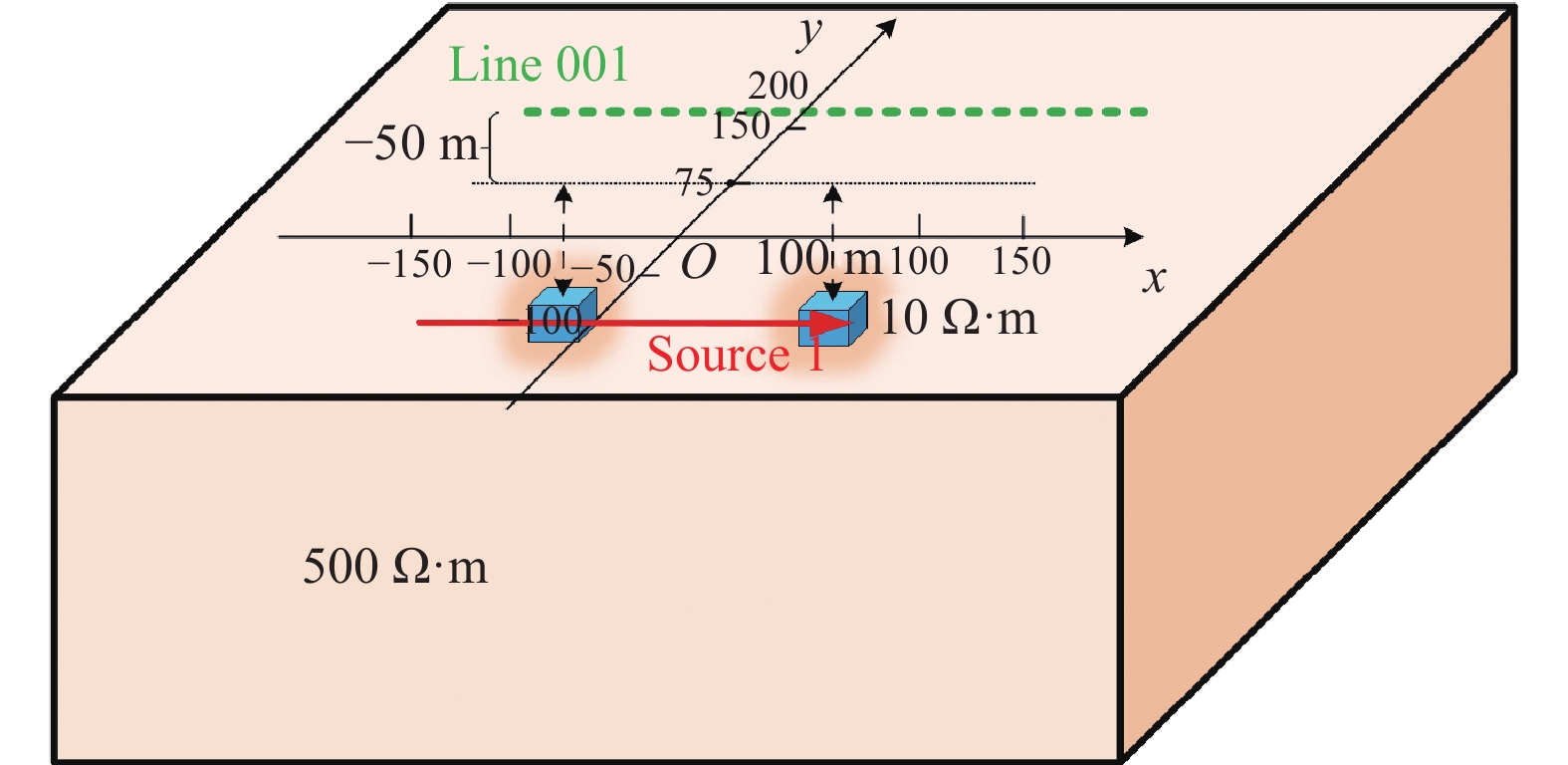
采用三维有限元正演方法对模型进行正演,通过改变源的位置与数量分析激发源的不同分布对瞬变场的影响。已知模型为电阻率$\rho = {\text{500}}\;\Omega \cdot {\rm{m}}$的均匀半空间中存在两个电阻率均为$1{\text{0}}\;\Omega \cdot {\rm{m}}$的块状低阻异常体,尺寸均为50 m×50 m×50 m,顶板埋深为100 m;发射参数为源长200 m,发射电流1 A(图1)。正演结果为飞行高度50 m处line001测线(y=75 m)磁场Z分量响应,磁场Z分量多测道曲线图显示为单峰曲线(图2)。
为了比较单辐射场源与多辐射场源地空瞬变电磁法之间的差异,现保持模型各参数不变,在对称位置增加场源且电流方向与原场源方向相反,源布置方式红色箭头线,源长为200 m,电流为1 A(图3)。正演计算结果为高程50 m处测线line1(y=75 m) 磁场Z分量数据(图4),对比图2与图4的多测道曲线可知,二者多测道曲线均表现为单峰形式,图4中多测道响应峰值大于图2中多测道响应峰值。由此可知,该类型源布置能提高数据的响应强度,这对于提高信噪比、压制电磁干扰等具有一定的意义。
继续保持模型参数不变,将激发源数量增至3条,源长度均为200 m,电流为1 A(图5)。完成正演计算后提取高程50 m处测线line1 Z分量数据。Line1(y=75 m)测线的磁场Z分量多测道图表现为双峰曲线,且最大值位置与异常体位置对应(图6)。对比图2、图4与图6,采用3条激发源以后不仅响应峰值得到了进一步加强,而且双峰对应的两个低阻异常平面位置与模型平面位置一致,说明复杂激发源可以提高探测分辨率,克服电性源体积效应影响。
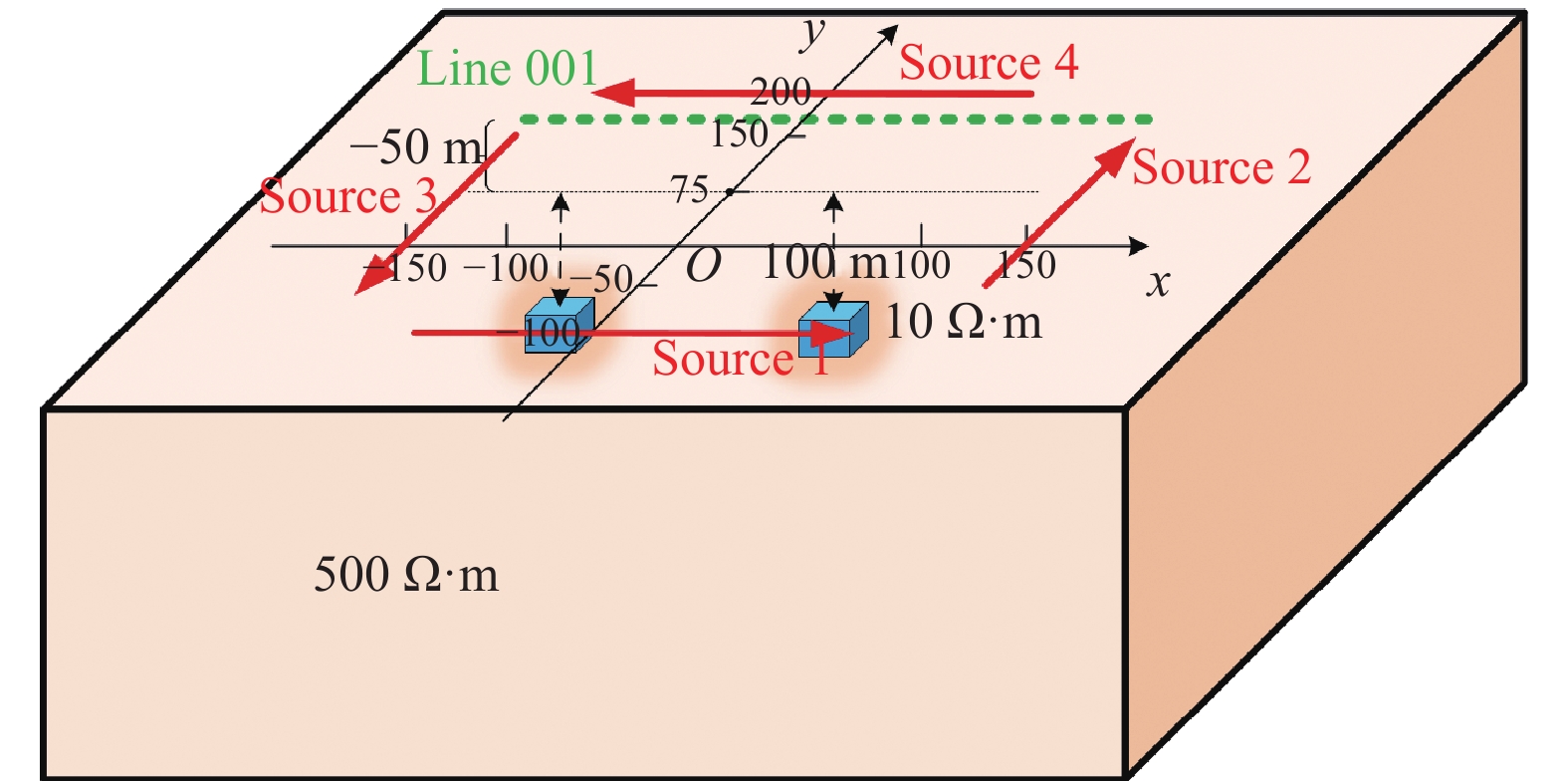
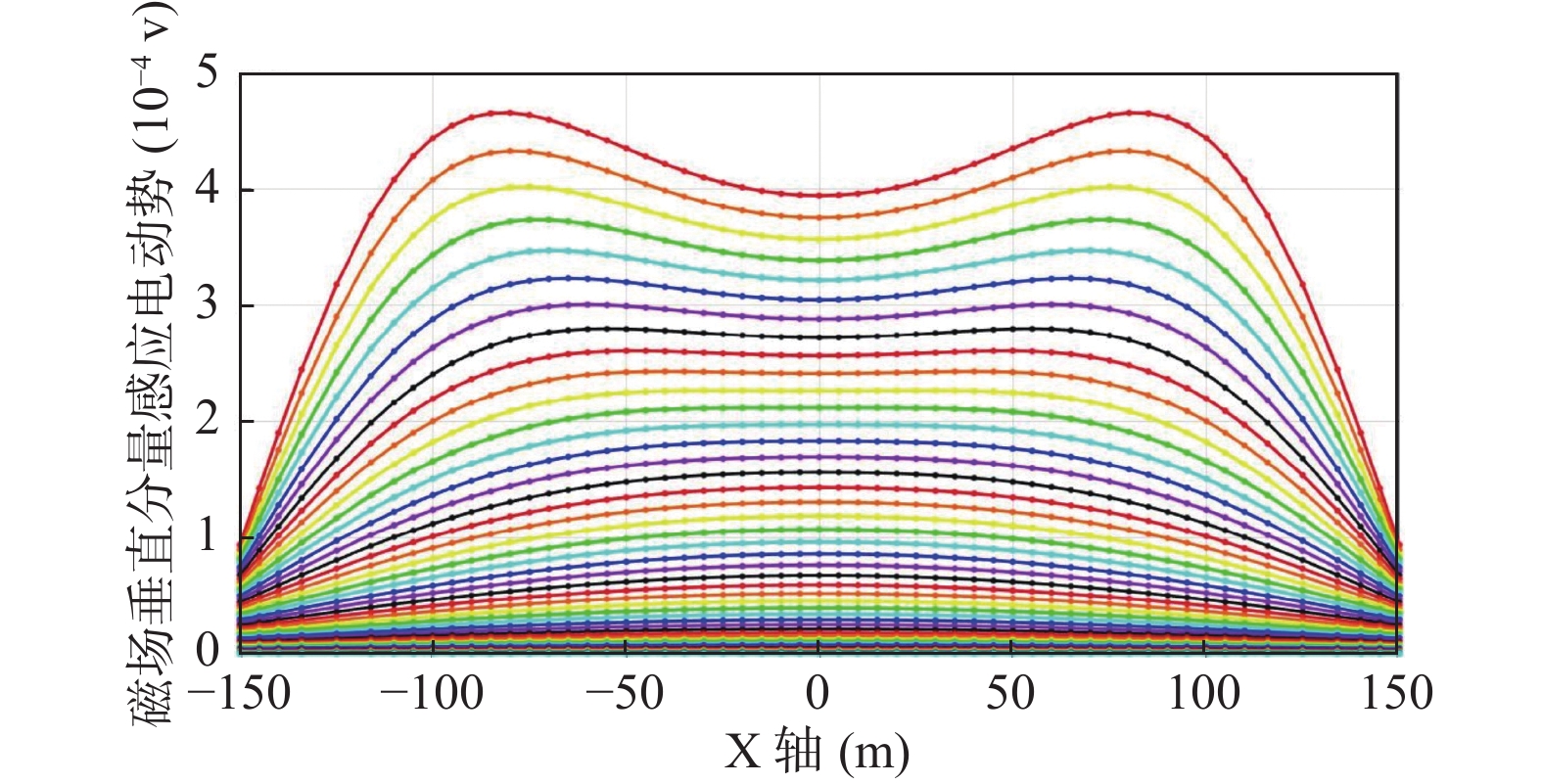
将激发源数量增加至4条,长度均为200 m,电流为1 A,其他参数不变(图7)。正演计算后提取高程50 m处测线line1(y=75 m) Z分量数据多测道曲线的双峰峰值持续增加(图8),与图6中曲线形态一致。对比图2、图4、图6与图8的多测道曲线,采用3个源以后瞬变响应在曲线形态上,可以对地下低阻异常体特征进行定性分析,而采用单个源或者平行双源仅能获得单峰曲线,很难从曲线形态上分析地下低阻异常体特征。
2. 多源地空瞬变电磁一维反演
阻尼最小二乘是一种成熟的反演方法,在地球物理反演中得到了广泛的应用(薛国强, 2008;周道卿, 2010)。笔者采用阻尼最小二乘法实现地空瞬变电磁反演,其中正演算法采用电性源层状模型瞬变电磁公式进行正演计算,利用全域视电阻率定义构建反演初始模型。
2.1 多源地空瞬变电磁一维反演原理
对于电性源地空瞬变电磁法最小二乘反演,构建如式(5)所示目标函数(李貅, 2002)
$$ \Phi \left[ {{\rho _1}, \cdots \cdots , {\rho _m}, {h_1}, \cdots \cdots , {h_{m - 1}}} \right] = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left[ {\frac{{{{\hat F}^{(i)}} - F(i{\mathbf{\bar P}})}}{{{{\hat F}^{(i)}}}}} \right]}^2}} $$ (5) 其中, $ {\hat F^{(i)}} $表示第$ i $个采样时间道的视电阻率,$ F(i\overline P ) $表示用模型参数$ \overline P $计算的第$ i $个采样时间道的视电阻率,$ n $为总的采样时间道数,$ \overline P $为理论模型参数,$ m $为地层层数,$ {\rho _i} $和$ {h_i} $分别为第$ i $层的电阻率和层厚。对(5)式进行泰勒展开,取$ {{\partial \Phi } \mathord{\left/ {\vphantom {{\partial \Phi } {\partial \Delta {P_j} = 0}}} \right. } {\partial \Delta {P_j} = 0}} $,得
$$ ({{\mathbf{A}}^{\mathbf{T}}}{\mathbf{A)}} \cdot {\mathbf{\Delta P = }}{{\mathbf{A}}^{\mathbf{T}}}{\mathbf{B}} $$ (6) 其中$ A = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{{\hat F}^{(1)}}}}\dfrac{{\partial F(1, {{\mathbf{P}}^{(0)}})}}{{\partial {\rho _1}}}}&{ \cdots }&{\dfrac{1}{{{{\hat F}^{(1)}}}}\dfrac{{\partial F(1, {{\mathbf{P}}^{(0)}})}}{{\partial {P_{2m - 1}}}}} \\ { \cdots }&{ \cdots }&{ \cdots } \\ {\dfrac{1}{{{{\hat F}^{(n)}}}}\dfrac{{\partial F(n, {{\mathbf{P}}^{(0)}})}}{{\partial {\rho _1}}}}&{ \cdots }&{\dfrac{1}{{{{\hat F}^{(n)}}}}\dfrac{{\partial F(n, {{\mathbf{P}}^{(0)}})}}{{\partial {P_{2m - 1}}}}} \end{array}} \right] $
$$ B = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{{\hat F}^{(i)}} - F(1, {{\mathbf{P}}^{(0)}})}}{{{{\hat F}^{(i)}}}}} \\ { \cdots } \\ {\dfrac{{{{\hat F}^{(n)}} - F(n, {{\mathbf{P}}^{(0)}})}}{{{{\hat F}^{(n)}}}}} \end{array}} \right]\;\;{\mathbf{\Delta P}} = \left[ {\begin{array}{*{20}{c}} {\Delta {P_1}} \\ { \cdots } \\ {\Delta {P_{2m - 1}}} \end{array}} \right]$$ 为了保证稳定收敛并加快收敛速度,添加阻尼因子$ \alpha $,构成如下所示LMF法方程
$$ ({{\mathbf{A}}^{\mathbf{T}}}{\mathbf{A}}{\text{ + }}\alpha {\mathbf{I)}} \cdot {\mathbf{\Delta P = }}{{\mathbf{A}}^{\mathbf{T}}}{\mathbf{B}} $$ (7) 在算法实现中,选择合适的$ \alpha $,达到调整搜索方向和步长的目的,获取模型的最优解。式(7)中雅可比矩阵元素的计算可采用差分法。由于马奎特方法适用于局部寻优,文中将全域视电阻率的结果作为反演的初始模型, 给定比较接近真实情况的初始模型。
2.2 多源地空瞬变电磁一维正演与视电阻定义
正演是反演的基础,文中基于电偶极子一维层状介质正演算法实现多源地空瞬变电磁的正演。已知电偶极子源地空瞬变电磁法的一维正演计算方程如下:
$$ {B_z}(\omega ) = \frac{{{P_E}}}{{2\pi }}{\mu _0}\sin \varphi \int_0^\infty {\frac{{{\lambda ^2}}}{{\lambda + {{{u_1}} \mathord{\left/ {\vphantom {{{u_1}} {{R_1}}}} \right. } {{R_1}}}}}{e^{\lambda z}}{J_1}(\lambda r)d\lambda } $$ (8) 其中,${u_i} = \sqrt {{\lambda ^2} + k_i^2} $,${k_i} = \sqrt { - i\omega {\mu _0}{\sigma _i}} $是介质的波数;${\sigma _i}$为第$ i $层介质的电导率,$ i = 1, 2, \ldots, m $;一般取$\mu = {\mu _{\text{0}}}$,${P_E} = Ids$为电偶极矩;$ I $是电流大小;$ ds $ 是发射源长度;$ z $是接收机高度。
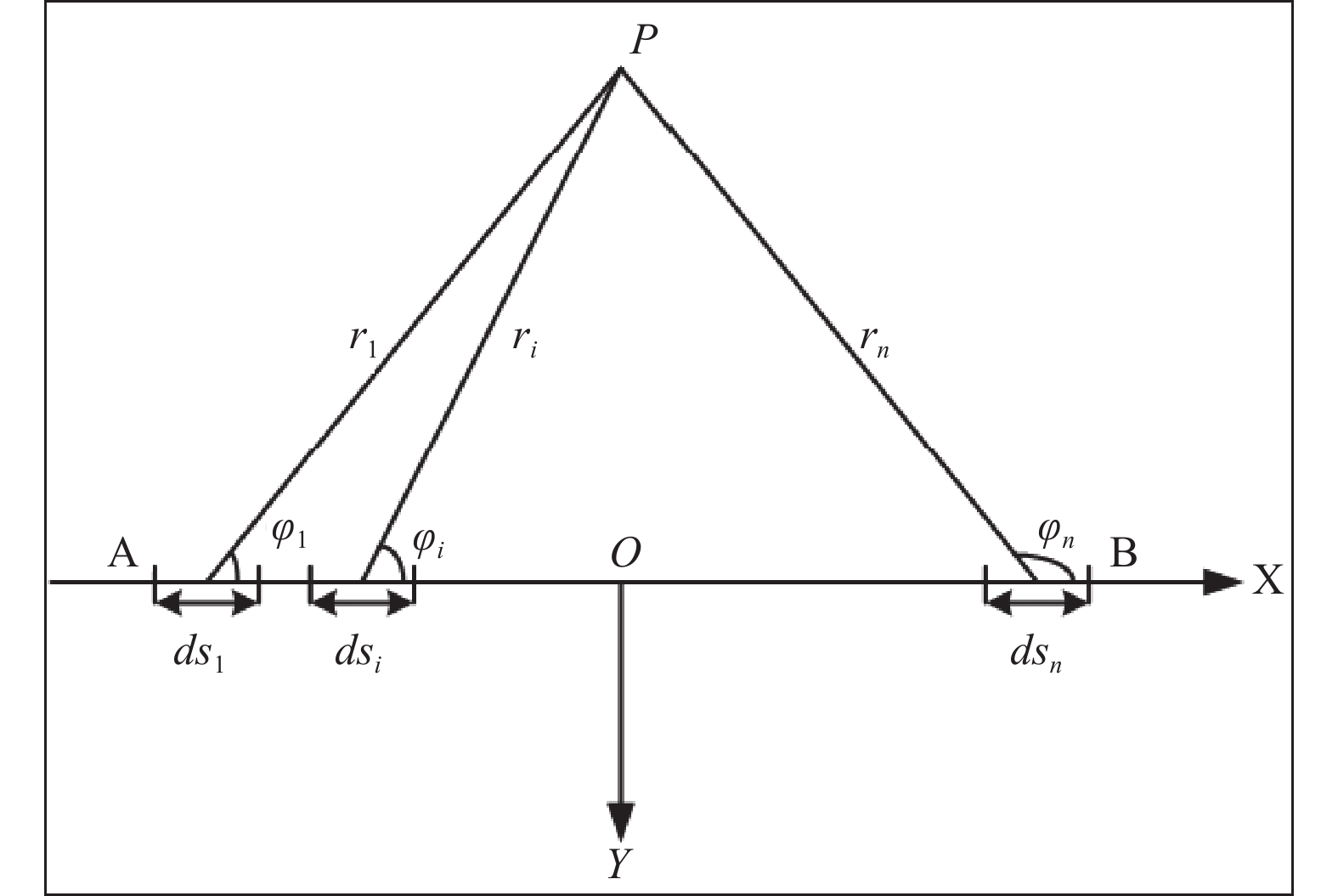
根据式(8)可得到电偶极子源频率域磁感应强度的分量响应。在实际工作中需铺设多个长导线源,不能简单将长导线源等效为电偶极子。首先,将第j条长导线源剖分成n段长度为ds的偶极子,再将各个偶极子在某测点处产生的频域场叠加起来,可得到整个长导线源的频域响应(图9)。而多辐射源可以看成多个电性源的叠加,分别计算出每个长导线源自身坐标系下所产生的频率域响应大小,通过叠加得到多辐射源整体的频率域响应,最后再利用频率域与时间域响应之间的转换关系(11)将多辐射源的频率域响应转换成时间域响应实现了多源地空瞬变电磁一维正演(张莹莹, 2016)。
$$ B_{\text{z}}^{\text{j}}(\omega ) = \sum\limits_{i = 1}^n {d{B_{zi}}(\omega )}$$ (9) $$ {B_{\text{z}}}(\omega ) = \sum\limits_{j = 1}^{{m}} {B_{\text{z}}^{\text{j}}(\omega )} $$ (10) 当采用阶跃电流发射时,频率域响应和时间域响应存在如下对应关系,一维正演过程采用线性数字滤波方法完成,再根据式(11)得到时间域响应(李貅,2002)。
$$ {B_z}(t) = \frac{2}{\pi }\int_0^\infty {\frac{{{Im} {B_z}(\omega )}}{\omega }} \cos (\omega t)d\omega $$ (11) 将时间域磁感应强度的z分量记为${B_z}(\rho, C, t)$,其中$ C $表示测点在空中的位置坐标参数。给定初值$\rho _\tau ^{\left( {\text{0}} \right)}$,在$\rho _\tau ^{\left( {\text{0}} \right)}$的邻域内对${B_z}(\rho, C, t)$进行泰勒展开并保留前两项后,
$$ {B_z}(\rho, C, t) \approx {B_z}(\rho _\tau ^{(0)}, C, t) + {B_z}^\prime (\rho _\tau ^{(0)}, C, t)(\rho - \rho _\tau ^{(0)}) $$ (12) 则视电阻计算可以写成迭代格式,如式13所示:
$$ \rho _\tau ^{(i + 1)} \approx \Delta \rho _\tau ^{(i)} + \rho _\tau ^{(i)}(i = 0, 1, 2, \cdots ) $$ (13) 其中,
$$ \Delta \rho _\tau ^{(i)} = \frac{{{B_z}(\rho, C, t) - {B_z}(\rho _\tau ^{(i - 1)}, C, t)}}{{{B_z}^\prime (\rho _\tau ^{(i - 1)}, C, t)}} $$ 迭代终止条件为
$$ \left| {\frac{{{B_z}(\rho, C, t) - {B_z}(\rho _\tau ^{(i)}, C, t)}}{{{B_z}(\rho, C, t)}}} \right| < \varepsilon $$ 2.3 算法验证
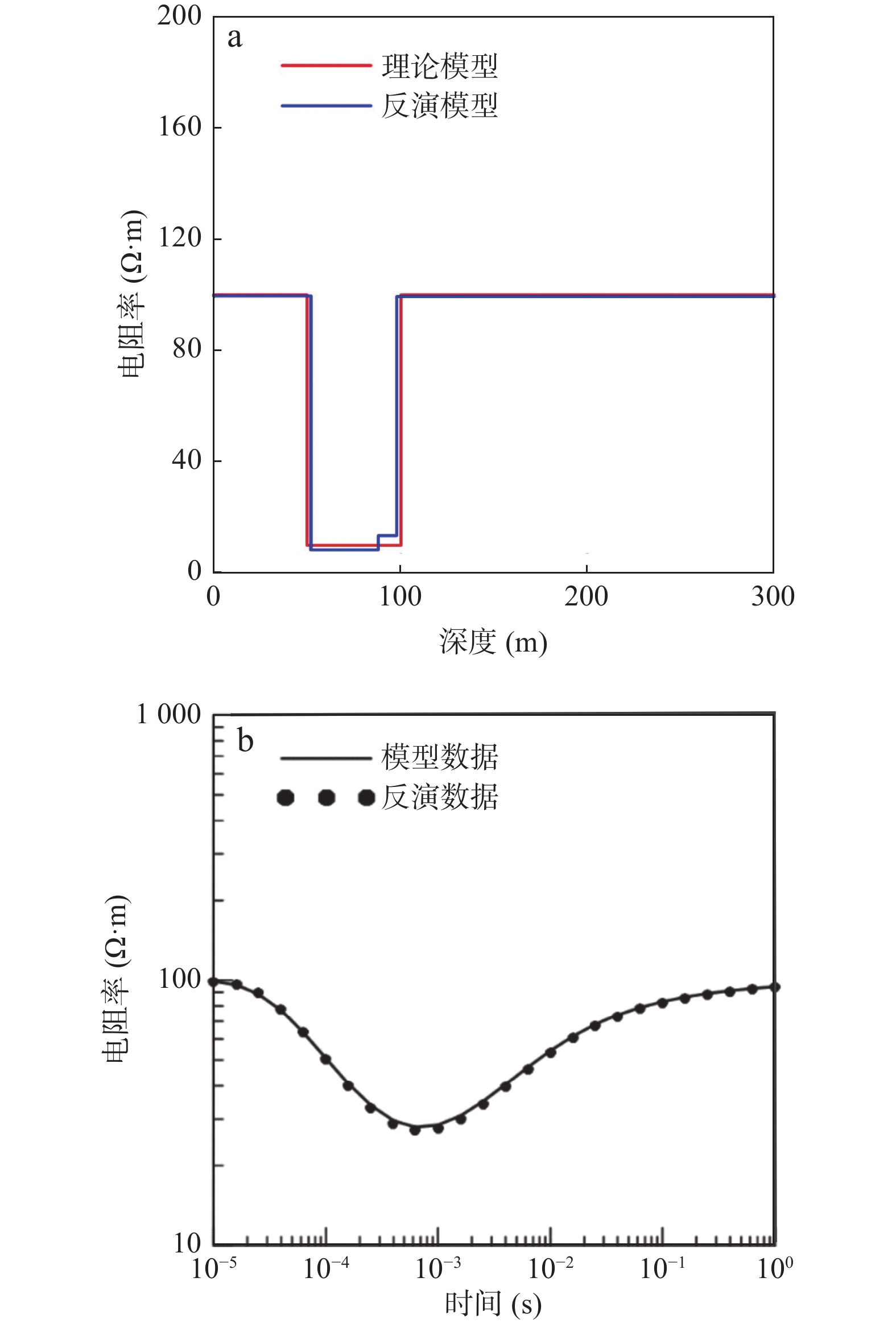
为了验证反演算法的正确性,运用文中算法对几个典型的层状模型进行反演。发射源参数为源长500 m,电流30 A,测点位置(300 m, 400 m, −100 m)。H型模型的电阻率为$ {\rho _{\text{1}}} = {\text{100}}\;\Omega \cdot {\rm{m}} $,$ {\rho _{\text{2}}} = {\text{10}}\;\Omega \cdot {\rm{m}} $,$ {\rho _{\text{3}}} = {\text{100}}\;\Omega \cdot {\rm{m}} $;层厚为$ {h_{\text{1}}} = 50\;{\rm{m}} $,${h_{\text{2}}} = 50\;{\rm{m}}$,该模型拟合结果较好(图10),拟合误差约为0.2%。
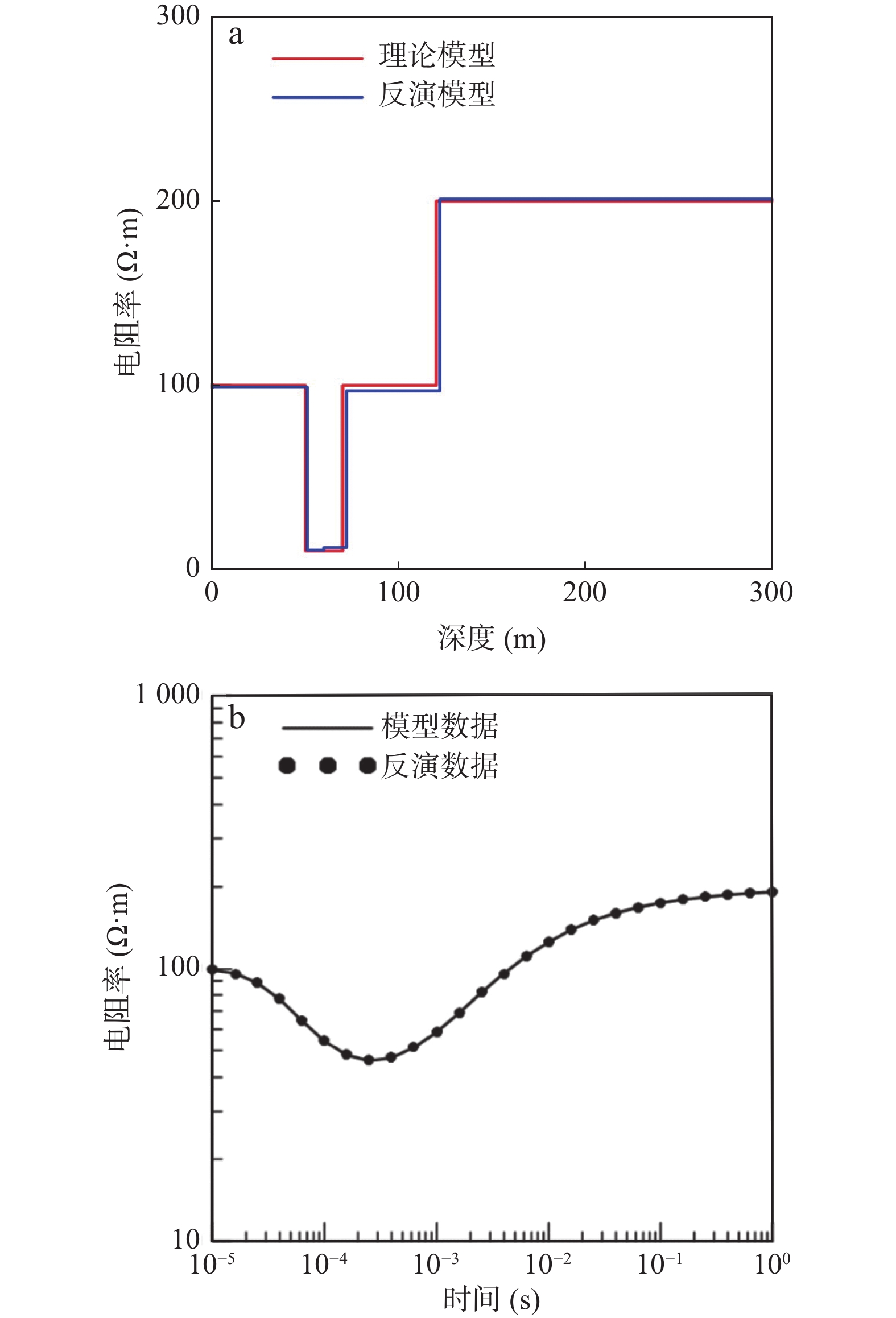
HA模型电阻率为$ {\rho _{\text{1}}} = {\text{100}}\;\Omega \cdot {\rm{m}} $,$ {\rho _{\text{2}}} = {\text{10}}\;\Omega \cdot {\rm{m}} $,$ {\rho _{\text{3}}} = {\text{100}}\;\Omega \cdot {\rm{m}} $,${\rho _4} = {\text{200}}\;\Omega \cdot {\rm{m}}$;层厚为$ {h_{\text{1}}} = 50\;{\rm{m}} $,${h_{\text{2}}} = 20\;{\rm{m}}$,${h_3} = 50\;{\rm{m}}$,该模型拟合结果更好(图11),拟合误差约为0.1%。
由于初始模型的选择借鉴了全域视电阻率的结果,并在反演过程中加入可行方向法,有效降低了反演问题的多解性,反演结果的电性界面清晰,且与理论模型对应较好,证明了反演方法的准确性。
3. 基于一维反演的三维模型数据分析
3.1 单源地空瞬变电磁一维反演
实际的探测中,并不能理想地将异常体或地质体看作均匀层状模型,而更多更广泛存在的是三维模型体,所以有必要研究三维模型的反演结果。设计了以下三维模型进行分析:背景电阻率为500 Ω·m,两个低阻目标体电阻率为10 Ω·m,尺寸为50 m×50 m×50 m的立方体,顶板埋深为70 m,另一个是倾斜的块状体,顶板埋深为50 m(图12)。
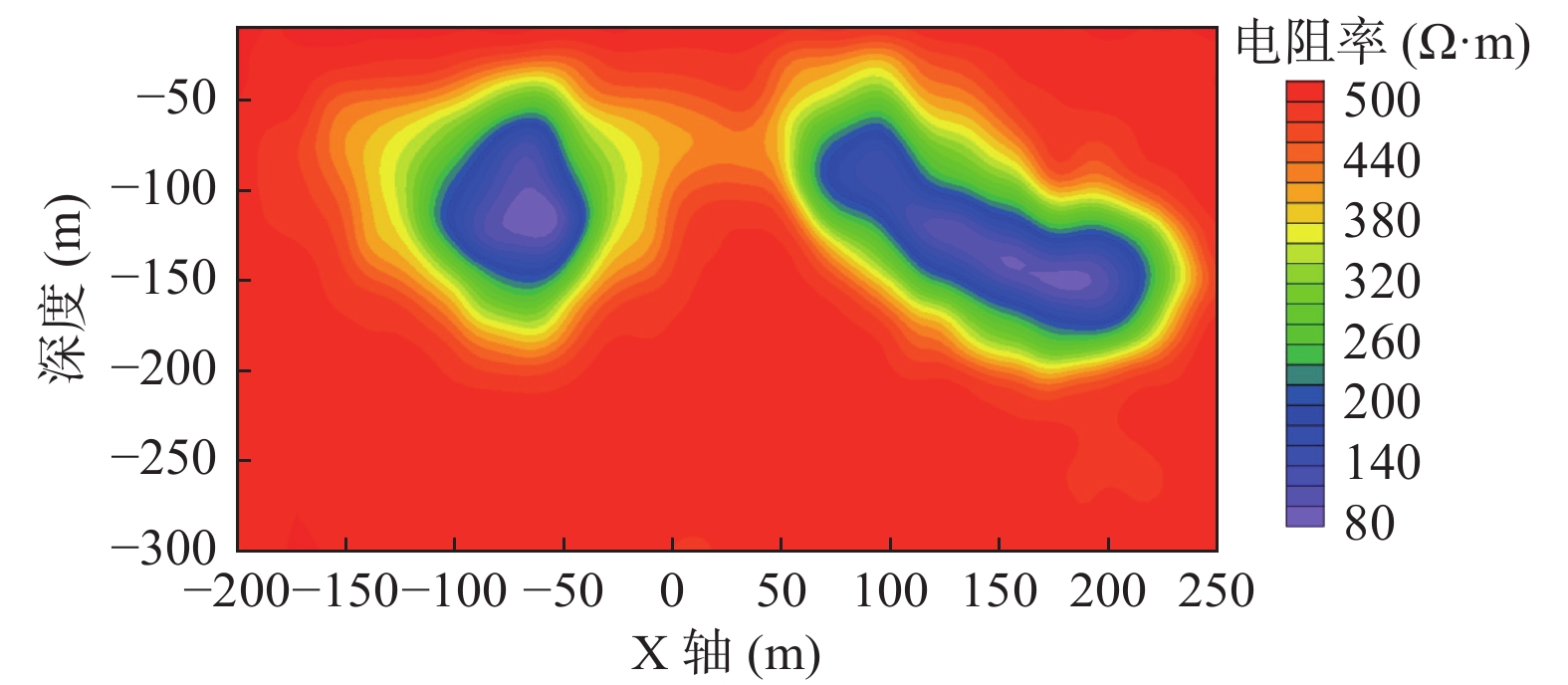
为了便于对多辐射源的特征进行分析,首先给出单辐射场源的反演结果。发射源与x轴平行放置,中心点为(0, −100),源长400 m,发射电流为10 A(图12)。反演的初始模型和约束条件的选择参照全域视电阻率结果,深度通过等效导电平面进行标定,反演的最终结果不能有效区分两个低阻异常(图13)。
3.2 多源地空瞬变电磁一维反演
保持模型不变,单源变为多源,源长度均为400 m,发射电流均为10 A(图14)。反演的初始模型和约束条件的不变,反演最终结果能够有效区分两个低阻异常(图15)。
对比图13与图15,采用多辐射源瞬变电磁探测方法对低阻目标体具有更好的分辨能力,可以给出较为详细的地下电阻率分布特征,全面地反映地下异常体信息,这也进一步说明复杂激发源简单的解释可以提高探测的分辨率。
4. 实例分析
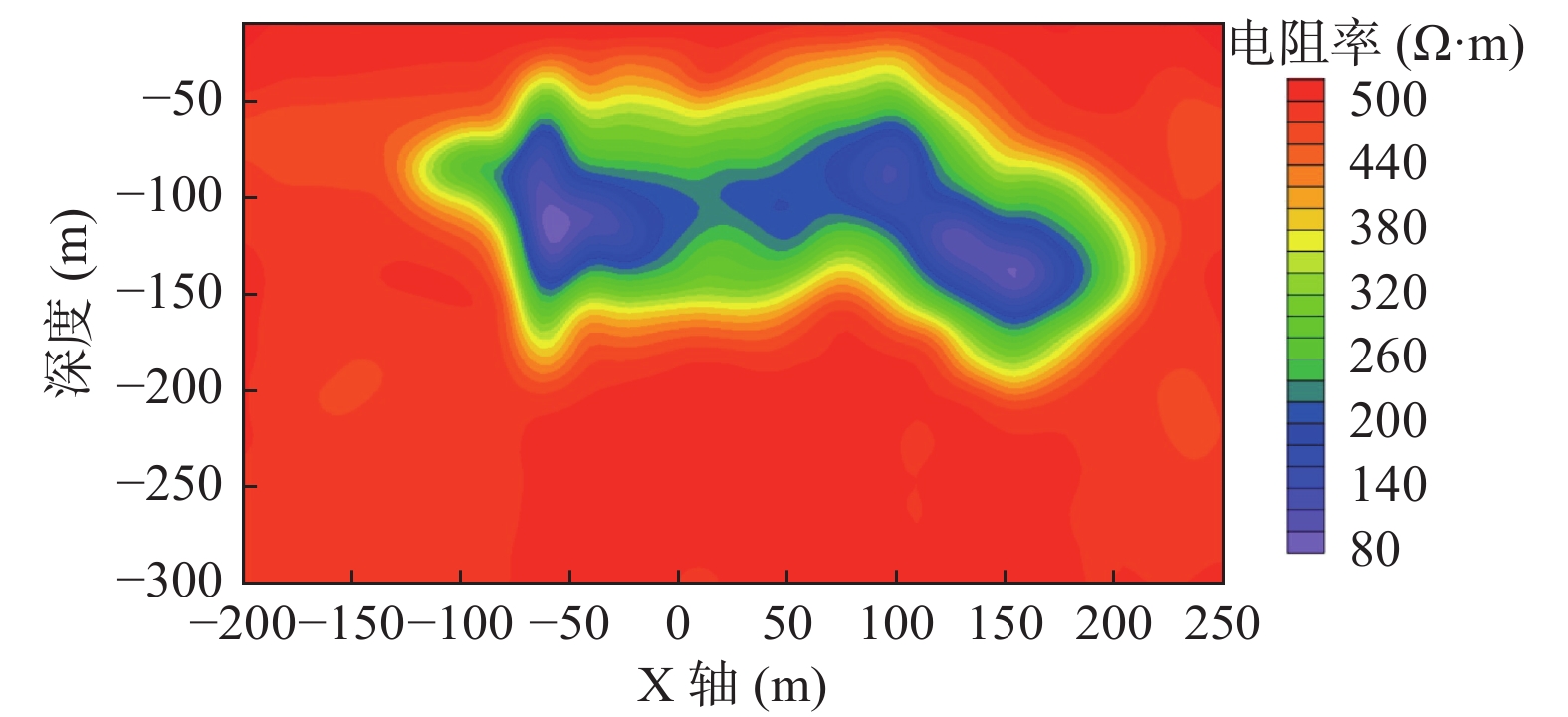
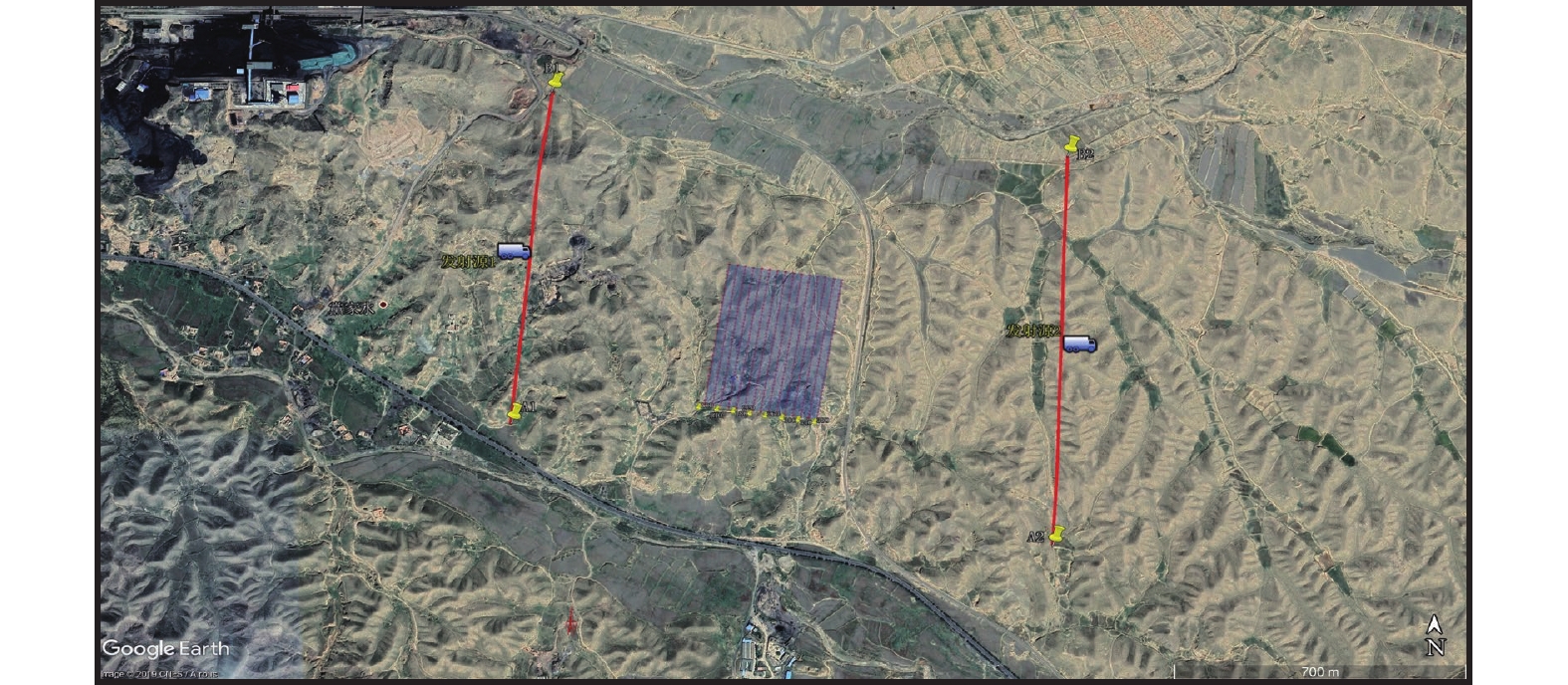
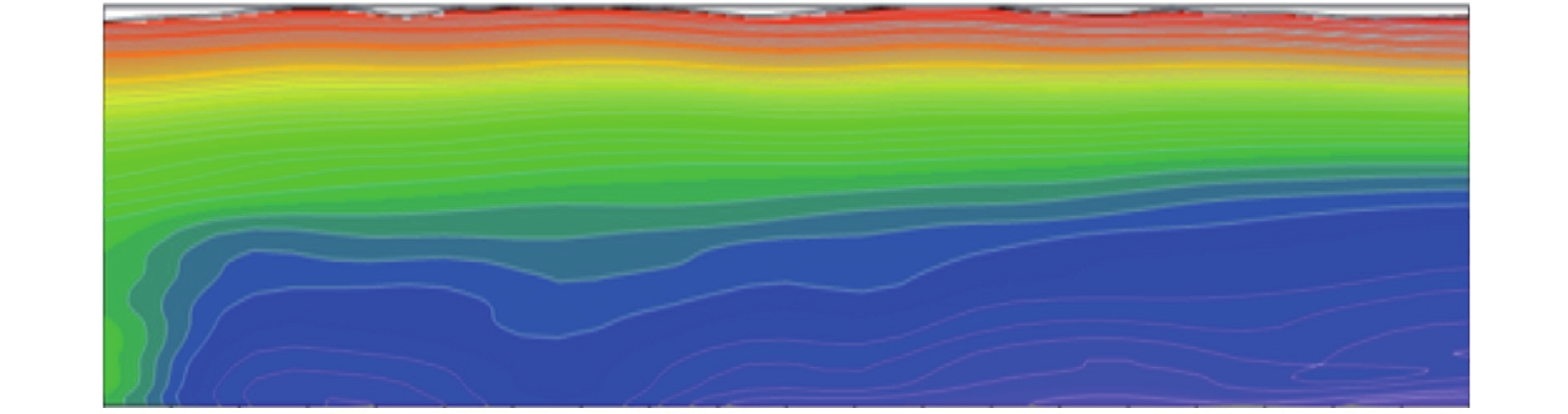
对甘肃某矿区采空区实测数据进行分析,激发源设置两个长度均为1 000 m,发射电流15 A(图16)。在探测过程中分别进行了单激发源和双激发源数据采集,将两种数据处理结果进行对比分析。首先对其中1条测线衰减电压的垂直分量进行视电阻率计算,利用所得结果对初始模型进行约束,深度通过等效导电平面标定,然后利用一维反演进行处理。
对比图17与图18,多发射源比单发射源可以对含水采空区的低阻区域有更好的分辨效果,可以给出更加详细的地下电阻率的分布特征,更全面地反映地下异常体信息,这也进一步说明了复杂激发源可以有效提高探测的分辨率,同时也证明一维反演多辐射源瞬变电磁数据在煤炭含水采空区探测中的有效性。
5. 讨论
(1)复杂辐射源瞬变电磁响应模型与野外实测数据的一维反演对比可以得出:多辐射源的正演结果和反演结果均能反映出更加详细的电阻率分布信息,有效提高了瞬变电磁法的分辨能力,有助于更好地了解地下的电性特征。
(2)文中模型采用磁场垂直分量与时间的导数信息:通过在空中接收衰减可以实现复杂激发源地空瞬变电磁数据采集,不仅能够提高工作效率,还能提高数据采样密度。通过增加源的布置方式,利用简单的解释方法实现较高精度的数据解释。
(3)本研究还存在的局限性以及进一步研究的建议:尽管多辐射源地空瞬变电磁法在理论上具有明显优势,但其实际应用仍面临一些挑战,如设备成本高、操作复杂等。未来的研究应致力于降低设备成本,简化操作流程,同时加强对多辐射源地空瞬变电磁法的理论研究,以提高其在实际勘探中的应用效率和准确性。
6. 结论
(1)本研究通过分析单源、双源、三源以及四源正演响应特征,揭示了增加发射源数量可以有效提高电磁响应强度的原理。当发射源增加到3~4个后,多测道曲线能够显示双异常体引起的电磁响应,说明3个发射源及以上能够减少长导线源的体积效应影响,提高方法的分辨率。
(2)研究中未发现明显的例外情况,但尚需解决的问题包括进一步优化多辐射源瞬变电磁法在复杂地质条件下的应用效果,并探索更高效的反演算法以提高数据解释精度。与以前发表的论文相比,本研究在理论和实践上提供了新的视角,特别是在提高瞬变电磁波分辨能力方面。
(3)建议未来的研究应集中于以下几个方向:①开发适用于不同地质条件的多辐射源瞬变电磁法快速成像方法。②利用三维数值模拟进一步验证和优化多辐射源瞬变电磁响应特征。③结合定量化、自动化、可视化等技术手段,提升地空瞬变电磁资料解释的准确性。
-
-
嵇艳鞠, 王远, 徐江, 等. 无人飞艇长导线源时域地空电磁勘探系统及其应用[J]. 地球物理学报, 2013, 56(11): 3640−3650. JI Yanju, WANG Yuan, XU Jiang, et al. Development and application of the grounded long wire source airborne electromagnetic exploration system based on an unmanned airship[J]. Chinese Journal of Geophysics,2013,56(11):3640−3650.
李肃义, 林君, 阳贵红, 等. 电性源时域地空电磁数据小波去噪方法研究[J]. 地球物理学报, 2013, 56(9): 3145−3152. LI Suyi, LIN Jun, YANG Guihong, et al. Ground-Airborne electromagnetic signals de-noising using a combined wavelet transform algorithm[J]. Chinese Journal of Geophysics,2013,56(9):3145−3152.
李貅, 胡伟明, 薛国强. 多辐射源地空瞬变电磁响应三维数值模拟研究[J]. 地球物理学报, 2021, 64(2): 716−723. LI Xiu, HU Weiming, XUE Guoqiang. 3D modeling of multi-radiation source semi-airborne transient electromagnetic response[J]. Chinese Journal of Geophysics,2021,64(2):716−723.
李貅, 张莹莹, 卢绪山, 等. 电性源瞬变电磁地空逆合成孔径成像[J]. 地球物理学报, 2015, 58(1): 277−288. LI Xiu, ZHANG Yingying, LU Xushan, et al. Inverse Synthetic Aperture Imaging of Ground-Airborne transient electromagnetic method with a galvanic source[J]. Chinese Journal of Geophysics,2015,58(1):277−288.
李貅. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社, 2002. LI Xiu. Theory and application of transient electromagnetic sounding [M]. Xi'an: Shaanxi Science Technology Press, 2002.
薛国强, 李貅, 底青云. 瞬变电磁法正反演问题研究进展[J]. 地球物理学进展, 2008, 23(4): 1165−1172. XUE Guoqiang, LI Xiu, DI Qingyun. Research progress in TEM forward modeling and inversion calculation[J]. Progress in Geophysics,2008,23(4):1165−1172.
张莹莹, 李貅, 李佳, 等. 多辐射场源地空瞬变电磁法快速成像方法研究[J]. 地球物理学进展, 2016, 31(2): 869−876. ZHANG Yingying, LI Xiu, LI Jia, et al. Fast imaging technique of multi-source ground-airborne transient electromagnetic method[J]. Progress in Geophysics,2016,31(2):869−876.
周道卿, 谭林, 谭捍东, 等. 频率域吊舱式直升机航空电磁资料的马奎特反演[J]. 地球物理学报, 2010, 53(2): 421−427. ZHOU Daoqing, TAN Lin, TAN Handong, et al. Inversion of frequency domain helicopter-borne electromagnetic data with Marquardt’s method[J]. Chinese Journal of Geophysics,2010,53(2):421−427.
Allah S A, Mogi T, Ito H, et al. Three-dimensional resistivity modeling of GREATEM survey data from Kujukuri beach, Japan[J]. Proceedings of the 10th SEGJ International Symposium, 2011, 314-317.
Allah S A, Mogi T, Ito H, et al. Three-dimensional resistivity characterization of a coastal area: application of grounded electrical source airborne transient electromagnetic(GREATEM) survey data from Kujukuri beach, Japan[J]. Journal of Applied Geophysics,2013,99:1−11. doi: 10.1016/j.jappgeo.2013.09.011
Bryan W, Roger E,Trenton. Resistivity Arrays as an Early Warning System for Monitoring Runoff Holding Ponds[J]. Journal of Environmental and Engineering Geophysics,2015,20:319−335. doi: 10.2113/JEEG20.4.319
Ito H, Mogi T, Jomori A, et al. Further invertigations of underground resistivity structures in coastal areas using grounded source airborne edectromagnetics[J]. Earth Planets and Space,2011,63(8):9−12. doi: 10.5047/eps.2011.08.003
Ito H, Kaieda H, Mogi T, et al. Grounded electrical-source airborne transient electromagnetic (GREATEM) survey of Aso Volcano, Japan[J]. Exploration Geophysics (CSIRO PUBLISHING),2014,45(1):43−48. doi: 10.1071/EG12074
Mogi T, Tanaka Y, Kusunoki K, et al. Development of grounded electrical-source airborne transient EM (GREATEM)[J]. Exploration Geophysics,1998,29:61−64. doi: 10.1071/EG998061
Mogi T, Kusunoki K, Kaieda H, et al. Grounded electrical-source airborne transient electromagnetic (GREATEM) survey of Mount Bandai, north-eastern Japan[J]. Exploration Geophysics,2009,40:1−7. doi: 10.1071/EG08115
Smith R S, Annan A P, McGowan P D. A comparison of data from airborn, semi-airborne, and ground electromagnetic sounding method[J]. Geophysics,2001,66(5):1379−1385. doi: 10.1190/1.1487084
Wright D A, Ziolkowski. Hydrocarbon detection and monitoring with a multicomponent transient electromagnetic (MTEM) survey[J]. The Leading Edge,2002,21:852−864. doi: 10.1190/1.1508954



 下载:
下载: